MÉTODO DE GAUSS

 MÉTODO GAUSS - JORDAN 

Para resolver un sistema de ecuaciones podemos, sin alterar las soluciones del sistema:

1. Intercambiar el orden de las ecuaciones.
2. Sumar algunas de sus ecuaciones.
3. Multiplicar alguna ecuación por un número distinto de 0.

Esto es precisamente lo que se hace en el método de Gauss: 

se modifican las ecuaciones para obtener un sistema mucho más fácil de resolver, pero, en lugar de hacerlo sobre las ecuaciones, se hace sobre la matriz ampliada del sistema. usa para determinar la inversa de una matriz y las soluciones de un sistema de ecuaciones lineales

El método de eliminación de Gauss consiste en operar sobre la matriz ampliada del sistema hasta hallar la forma escalonada (una matriz triangular superior). Así, se obtiene un sistema fácil de resolver por sustitución hacia atrás.

Si finalizamos las operaciones al hallar la forma escalonada reducida (forma lo más parecida a la matriz identidad), entonces el método se denomina eliminación de Gauss-Jordan.

EJEMPLO GAUSS - JORDAN 

La matriz ampliada del sistema es

A fila 1 le restamos dos veces la fila 3 y a la fila 2 le restamos la fila 3:

A la fila 1 le restamos la fila 2:

Dividimos la fila 1 entre 3:

A la fila 3 le sumamos la fila 1 y a la fila 2 le restamos dos veces la fila 1:

Dividimos la fila 2 entre 3:

A la fila 3 le sumamos la fila 2:

Reordenamos las 3 filas:

Ya tenemos resuelto el sistema porque la matriz obtenida es la solución:

         EJEMPLO GAUSS - JORDAN 

El sistema transformado en matriz: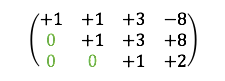

Si te fijas, ya podemos despejar directamente una de las incógnitas. Por tanto, este tipo de sistemas es muy fácil de resolver obteniendo el valor de las incógnitas de abajo hacia arriba. De esta manera, podemos ir sustituyendo los valores obtenidos en las anteriores.

z=2
Sustituimos el valor de “z” en la segunda ecuación y obtenemos el valor de “y”:
y+3.(2)=8;
 y=8-6=2
y=+2
 
Sustituimos el valor de “z” e “y” en la primera ecuación y obtenemos “x”:
 y=2
x+(2)+3.(2)=-8;
 x=-16

En este video podemos entender un poco mas a fondo sobre el método de gauss

• https://youtu.be/XRcx8-2lLJI

En este video podemos entender un poco mas a fondo sobre el método de gauss - Jordan

• https://youtu.be/dFmGzr1j6eY