METODO DE CRAMER
METODO DE CRAMER
- Debemos sacar el determinante de la matriz que llamaremos delta
- Para sacar el valor de x reemplazamos por los resultados de las ecuaciones, sacamos el determinante y dividimos el delta por el determinante de la matriz x
- Para sacar el valor de y reemplazamos por los resultados de las ecuaciones, sacamos el determinante y dividimos el delta por el determinante de la matriz y
- Para sacar el valor de z reemplazamos por los resultados de las ecuaciones, sacamos el determinante y dividimos el delta por el determinante de la matriz z
EJEMPLO
Sistema de dimensión 2x2:
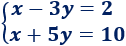
La matriz de coeficientes del sistema es
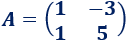
La matriz de incógnitas es
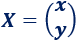
La matriz de términos independientes es
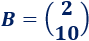
Calculamos el determinante de :
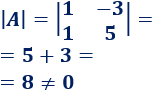
Podemos aplicar la regla de Cramer.
La primera incógnita es , cuyos coeficientes son los de la primera columna de . La matriz es como pero cambiando dicha columna por la columna :

Calculamos :
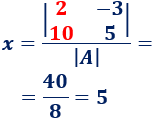
La segunda incógnita es y sus coeficientes son los de la segunda columna de . Tenemos que calcular el determinante de la matriz
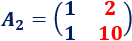
Calculamos :
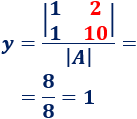
Por tanto, la solución del sistema es
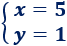
EJEMPLO
Sistema de dimensión 3x3:
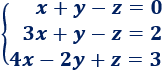
La matriz de coeficientes del sistema es

La matriz de incógnitas es
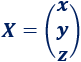
La matriz de términos independientes es
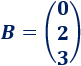
Calculamos el determinante de :
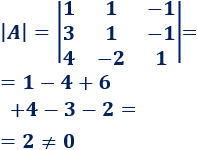
Podemos aplicar la regla de Cramer.
La matriz es como pero cambiando la columna 1 por la columna :

Calculamos :
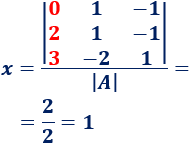
La matriz es como pero cambiando la columna 2 por la columna :

Calculamos :
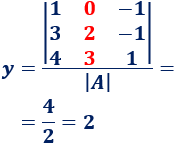
La matriz es como pero cambiando la columna 3 por la columna :
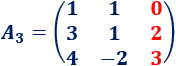
Calculamos :
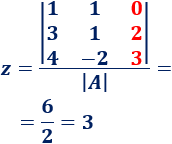
Por tanto, la solución del sistema es
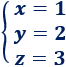

Comentarios
Publicar un comentario