COMBINACIONES LINEALES
COMBINACIONES LINEALES
Una combinación lineal de dos o más vectores es el vector que se obtiene al sumar esos vectores multiplicados por algunos escalares. Es decir, una combinación lineal es una expresión de la forma:
Para ser una combinación lineal el sistema debe tener una única solución
EJEMPLO
EJEMPLO 2
Dados los siguientes vectores:
Expresa el vector u como combinación lineal de v y w.
Solución
Empezamos sustituyendo los vectores por sus coordenadas:

Multiplicamos cada coeficiente por las coordenadas de los vectores en el segundo miembro:
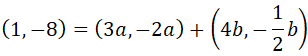
Operamos en cada una de las coordenadas:
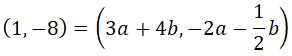
Y por último igualamos coordenadas en ambos miembros, dando lugar al siguiente sistema de dos ecuaciones con dos incógnitas:
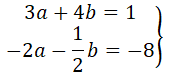
La solución de este sistema de ecuaciones es:
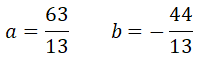
Por lo que el vector v expresado como combinación lineal de u y v queda de la siguiente forma:

EJEMPLO
EJEMPLO 2
Dados los siguientes vectores:
Expresa el vector u como combinación lineal de v y w.
Solución
Empezamos sustituyendo los vectores por sus coordenadas:

Multiplicamos cada coeficiente por las coordenadas de los vectores en el segundo miembro:
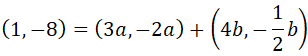
Operamos en cada una de las coordenadas:
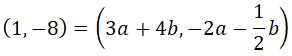
Y por último igualamos coordenadas en ambos miembros, dando lugar al siguiente sistema de dos ecuaciones con dos incógnitas:
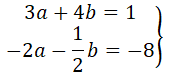
La solución de este sistema de ecuaciones es:
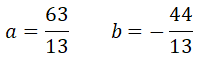
Por lo que el vector v expresado como combinación lineal de u y v queda de la siguiente forma:

EJEMPLO




Comentarios
Publicar un comentario