DETERMINANTES RANGO Y MENORES

La matriz determinante de una matriz cuadrada AA [A] [A] es una herramienta clave en el algebra.

 La matriz cuadrada de dimensión 2. calculamos el determinante restan el producto de los elementos de las diagonales:

 

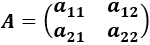
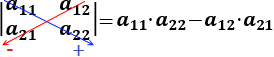
REGLA DE SARRUS

La matriz cuadrada de dimensión 3. calculamos el determinante mediante la llamada regla de Sarrus. Una forma de aplicar la regla de Sarrus es escribir las tres columnas de la matriz seguidas de la primer y la segunda columna:

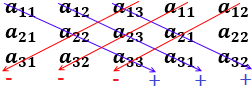
Los elementos de las diagonales con flecha hacia abajo (azul) se multiplican y se suman; los de las otras diagonales (rojo) se multiplican y se restan:

Ejemplo:

Ejemplo:

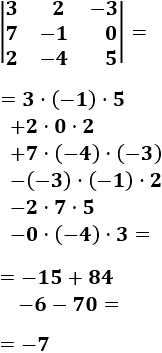
MATRIZ ADJUNTA

Para sacar el adjunto de una matriz debemos seleccionar la posición y eliminarle la fila y la columna, ejemplo:

REGLA DE LAPLACE

A regla de Laplace factoriza la matriz inicial en matrices de menor dimensión y ajusta su signo en función de la posición del elemento en la matriz. 

En esta regla escogemos una fila o una columna de la matriz y le sacamos la adjunta, a cada adjunta le sacamos el determinante y a cada determinante lo multiplicamos por el numero de la posición, lego afectamos con los signos de la matriz (+-+-+-+-).

Ejemplo:

Ejemplo: